Documentation on mori.x
The main purpose of mori.x is the computation of the Mori cone of toric varieties given by star triangulations of reflexive polytopes, which correspond to crepant subdivisions of the associated fans. The program is able to perform such triangulations for four-dimensional polytopes with up to three non-vertex points if the secondary fan is at most three--dimensional. The program can also be used with a known triangulation as its input starting from PALP release 2.1. This option, which was not contained in PALP 2.0 as described in arXiv:1106.4529, works for arbitrary dimensions.
Contents |
General aspects of mori.x
We distinguish two types of functionalities of mori.x. The first kind yields information about the appropriately resolved ambient space (see options ' -g, -I, -m, -P, -K' below). This includes the Stanley-Reisner (SR) ideal (with ' -g') as well as specific information on the geometry of the lattice polytope that determines the ambient toric variety: incidence structure of the facets ( '-I'), IP-simplices ( -P) and subdivisions of the fan ( '-g'); furthermore, the Oda-Park algorithm (see Oda, T. and Park, H. ,Linear Gale transforms and Gel'fand-Kapranov-Zelevinskij decompositions, as well as hep-th/9506091) is used to find the Mori cone of the ambient space ( '-m'). The second kind of functionalities deals with the intersection ring (' -i, -t') and topological quantities (' -b, -c, -d') of the embedded hypersurface. They are determined with the help of SINGULAR, a computer algebra system for polynomial computations. Correspondingly, the options ' -b, -i, -c, -t, -d' (as well as ' -a, -H', see below) need SINGULAR to be installed.
The generators of the Mori cone are given in terms of their intersections with the toric divisors. For singular toric varieties, the Picard group of Cartier divisors is a non-trivial subgroup of the Chow group, which contains the Weil divisors. Hence one can consider the Kähler cone, which is dual to the Mori cone, as a cone in the vector space spanned by the elements of either the Picard or the Chow group. The program mori.x only deals with simplicial toric varieties, for which the Picard group is always a finite index subgroup of the Chow group.
Hence the Cartier divisors are integer multiples of the Weil divisors and this ambiguity does not arise.
Starting with PALP 2.1, mori.x affords two distinct modes of operation. If used with the option -M arbitrary reflexive polytopes of any dimension can serve as input (at least in principle).
Without -M the program only works if the input polytope can be triangulated by mori.x or if it does not require triangulation, as we will outline in the following paragraphs.
As described in arXiv:1106.4529, mori.x can perform
star triangulations of certain four--dimensional reflexive polytopes. This operation was designed for the
CY hypersurface case. Generic CY hypersurfaces avoid point-like singularities of the ambient space as well as divisors that correspond to interior points of facets. Consequently,
the algorithm performs star triangulations only up to such interior points.
Polytopes can be triangulated by subdividing the secondary fans of its non-simplicial facets, see L.Billera, P.Filliman and B.Sturmfels, 'Constructions and complexity of secondary polytopes' as well as I.Gel'fand, M.Kapranov, A.Zelevinsky 'Discriminants, resultants, and multidimensional determinants', Birkhäuser Boston 2008.
This triangulation algorithm is implemented in mori.x for
polytopes with up to three points that are neither vertices nor interior to
the polytope or one of its facets;
this implies that the secondary fan of any facet can be at most
three-dimensional.
The program exits with a warning message if the subdivision is not properly
completed.
As the dimension of the secondary fan corresponding to a facet grows with the number of points in the facet, this limitation tends to become relevant for toric varieties for which h1,1 is large: h1,1 increases with the number of points on the polytope and polytopes with many points are more likely to have facets containing many points.
Complete triangulations of arbitrary polytopes can be performed with programs as TOPCOM, which is also included in the open source mathematics software system SAGE. SAGE also contains various tools for handling toric varieties. The triangulations performed in mori.x are attuned to the case of three-dimensional CY hypersurfaces. This means, in particular, that interior points of facets are ignored: one must use -M to avoid this. For small Picard numbers, mori.x is hence faster than programs which perform a complete triangulation.
If a polytope of arbitrary dimension has only simplicial facets whose only lattice points are its vertices and possibly interior points, it does not require any triangulation. Hence mori.x can also handle such cases without -M.
With the option '-H' the program can also analyze arbitrary hypersurfaces embedded in the ambient toric varieties. It is capable of computing the intersection ring and certain characteristic classes. Here the omission of interior points of facets, which happens as a consequence of mori.x's triangulation algorithm, may introduce severe singularities which often result in non--integer intersection numbers. There is a warning if there are indeed points interior to facets; in such a case it is probably better to repeat the computation with the combination '-HM'.
Help Screen
The help screen provides essential information about all the functionalities of the program:
palp$ mori.x -h
This is ``mori.x'':
star triangulations of a polytope P* in N
Mori cone of the corresponding toric ambient spaces
intersection rings of embedded (CY) hypersurfaces
Usage: mori.x [-<Option-string>] [in-file [out-file]]
Options (concatenate any number of them into <Option-string>):
-h print this information
-f use as filter
-g general output: triangulation and Stanley-Reisner ideal
-I incidence information of the facets (ignoring IPs of facets)
-m Mori generators of the ambient space
-P IP-simplices among points of P* (ignoring IPs of facets)
-K points of P* in Kreuzer polynomial form
-b arithmetic genera and Euler number
-i intersection ring
-c Chern classes of the (CY) hypersurface
-t triple intersection numbers
-d topological information on toric divisors &
del Pezzo conditions
-a all of the above except h, f, I and K
-D lattice polytope points of P* as input (default CWS)
-H arbitrary (also non-CY) hypersurface
`H = c1*D1 + c2*D2 + ...' input: coefficients `c1 c2 ...'
-M Stanley-Reisner ideal and Mori generators with an
arbitrary triangulation as input; must be combined with -D
Input: 1) standard: degrees and weights
`d1 w11 w12 ... d2 w21 w22 ...'
2) alternative (use -D): `d np' or `np d'
(d=Dimension, np=#[points]) and (after newline) np*d
coordinates
Output: as specified by options
Following PALP's notation we refer to the M lattice polytope which
determines the CY hypersurface as P; consequently its dual, which
gives rise to the fan of the ambient toric variety, is P * .
As PALP always interprets the input as 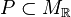 unless some
option
modifies this behavior, matrix input of
unless some
option
modifies this behavior, matrix input of 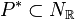 requires
the option '-D'.
In order to avoid errors, matrix input is not allowed unless this option is set.
If only Pbut not P * is known one can use 'poly.x -e' to obtain the
latter.
requires
the option '-D'.
In order to avoid errors, matrix input is not allowed unless this option is set.
If only Pbut not P * is known one can use 'poly.x -e' to obtain the
latter.
Options of mori.x
This section contains a detailed description of the options listed in the help screen. If no flag is specified, the program starts with the parameter '-g'. By default, the program considers a CY hypersurface embedded in the ambient toric variety. The option '-H' has to be used in order to consider non-CY hypersurfaces. Note that the options '-b, -i, -c, -t, -d, -a, -H' need SINGULAR to be installed.
Most options of mori.x produce output that is related to the points of P * in a specific order which can be determined by combining the desired functionality with the option '-P'. In order to avoid repeating this information for every option, we now present an example that will be used for many of the options below:
palp$ mori.x -P
Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...':
8 4 1 1 1 1 0 6 3 1 0 1 0 1
4 8 points of P* and IP-simplices
-1 0 0 0 1 3 1 0
0 0 0 1 0 -1 0 0
-1 1 0 0 0 3 1 0
1 0 1 0 0 -4 -1 0
------------------------------ #IP-simp=2
4 1 0 1 1 1 8=d codim=0
3 0 1 1 0 1 6=d codim=1
The output before the dashed line just means that P * has the lattice
points\footnote{Here the index
starts at 1instead of 0as it is standard in PALP.
This shift is needed to match the counting of toric divisor classes displayed
in certain outputs of mori.x and hence avoids confusion.
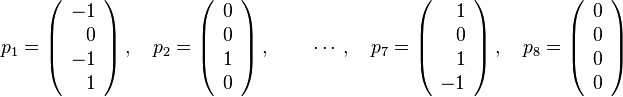
and the last two lines encode the facts 4p1 + p2 + p4 + p5 + p6 = 0,
3p1 + p3 + p4 + p6 = 0. Note how the dashed line proceeds only up to p6. This is because mori.x always ignores the origin, and, if used without -M, also ignores points that are interior to facets: p7 = (p2 + p4 + p5 + p6) / 4 = (p3 + p4 + p6) / 3 lies inside the facet with vertices p2,p3,p4,p5,p6. The reader is invited to check that the same example with 'mori.x -PM' results in a dashed line below all points except the origin.
-h
This option prints the help screen.
-f
This parameter suppresses the prompt of the command line. This is useful if one wants to build pipelines or shorten the input; e.g.~our standard example can be entered as
palp$ echo '8 4 1 1 1 1 0 6 3 1 0 1 0 1' | mori.x -fP 4 8 points of P* and IP-simplices ...
-g
This triggers the general output. First, the triangulation data of the facets is displayed. The number of triangulated simplices is followed by the incidence structure of the simplices. The incidence information for each simplex is encoded in terms of a bit sequence (cf. sec.~ Binary representation of incidences): there is a digit for each relevant polytope point; a 1 denotes that the point belongs to the simplex. Second, the SR ideal is displayed: the number of elements of the ideal is followed by its elements. Each element is denoted by a bit sequence as above.
palp$ echo '8 4 1 1 1 1 0 6 3 1 0 1 0 1' | mori.x -fg 8 Triangulation 110101 111100 101011 101110 100111 111001 001111 011101 2 SR-ideal 010010 101101 9 Triangulation 110101 111100 101011 101110 100111 111001 010111 011011 011110 2 SR-ideal 110010 001101
The program performs the two possible triangulations of the
facet 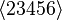 , which is the only non--simplicial one
(see section -I).
The last two bit sequences of the first result describe the simplices
, which is the only non--simplicial one
(see section -I).
The last two bit sequences of the first result describe the simplices
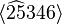 ,
whereas the second triangulation gives the three simplices
,
whereas the second triangulation gives the three simplices
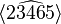 (in this notation the hat indicates that one of the points is dropped).
Nevertheless, the two resolutions give the same CY intersection polynomial.\footnote{This
fact suggests that the two resolutions give rise to the same CY hypersurface.
Indeed, simply connected CY threefolds are completely determined up to
diffeomorphisms by their Hodge numbers, intersection rings and second Chern
classes, see C. T. C. Wall, 'On certain 6-manifolds and
arXiv:0802.3376.
(in this notation the hat indicates that one of the points is dropped).
Nevertheless, the two resolutions give the same CY intersection polynomial.\footnote{This
fact suggests that the two resolutions give rise to the same CY hypersurface.
Indeed, simply connected CY threefolds are completely determined up to
diffeomorphisms by their Hodge numbers, intersection rings and second Chern
classes, see C. T. C. Wall, 'On certain 6-manifolds and
arXiv:0802.3376.
-I
The incidence structure of the facets of the polytope P * is displayed. Interior points of the facets are neglected.
palp$ echo '8 4 1 1 1 1 0 6 3 1 0 1 0 1' | mori.x -fI Incidence: 110101 111100 011111 101011 101110 100111 111001
The incidence data show the intersections
of 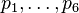 (ignoring p7, p8!)
with the seven facets. The third facet contains the
five points
(ignoring p7, p8!)
with the seven facets. The third facet contains the
five points 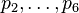 , hence it is not simplicial and
needs to be triangulated. See paragraph Binary representation of incidences for more details on the
representation of incidences as bit sequences.
, hence it is not simplicial and
needs to be triangulated. See paragraph Binary representation of incidences for more details on the
representation of incidences as bit sequences.
-m
The Mori cone generators of the ambient space are displayed in the form of a matrix.\footnote{As divisors corresponding to interior points of facets do not intersect a CY hypersurface, such divisors are neglected in the computation of the Mori cone of the ambient space.} Each row corresponds to a generator. The entries of each row are the intersections of the generator with the toric divisor classes. The Oda-Park algorithm is used to compute the generators. Furthermore, the incidence structure between the generators of the Mori cone and its facets is displayed. For the standard example this takes the following form.
palp$ echo '8 4 1 1 1 1 0 6 3 1 0 1 0 1' | mori.x -fm 2 MORI GENERATORS / dim(cone)=2 3 0 1 1 0 1 I:10 0 3 -4 -1 3 -1 I:01 2 MORI GENERATORS / dim(cone)=2 1 1 -1 0 1 0 I:10 0 -3 4 1 -3 1 I:01
The Mori cone is two-dimensional, so that its facets can be identified with the generators. This explains the trivial incidence structure.
Let us consider another simple
example, a hypersurface in 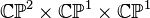 .
.
palp$ mori.x -m Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...': 3 1 1 1 0 0 0 0 2 0 0 0 1 1 0 0 2 0 0 0 0 0 1 1 3 MORI GENERATORS / dim(cone)=3 0 0 0 1 1 0 0 I:110 1 1 0 0 0 0 1 I:101 0 0 1 0 0 1 0 I:011
The Mori cone generators can easily be seen to be dual to the hyperplane sections. Now, the Mori cone is three-dimensional, so that each of its facets contains two generators. Let us, for instance, consider the incidence structure between the first generator and the three facets of the Mori cone. Here, the string 'I:110' tells that the vector lies on the first and second facets but does not intersect the third one.
For an example with a more complicated structure of the Mori cone see section -M.
-P
First a list of lattice points of P * is displayed in the following manner. If '-P' is combined with both -M and '-D', the list is just the input provided by the user, in the same order except for the fact that the lattice origin comes at the end of the list. In all other cases the complete list of lattice points of P * is given in the following order:
1. vertices (with '-D' in the order provided by the user),
2. points not interior to the polytope or its facets,
3. points interior to facets,
4. the lattice origin.
Then a dashed line indicates which points are `relevant': all points except for the origin in the case of -M, but not points interior to facets otherwise. Finally the IP-simplices with vertices among these relevant points are displayed.
The output for the standard example can be found in here.
As a further example consider a 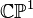 fibered over
fibered over 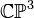 :
:
palp$ mori.x -P
Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...':
5 1 1 1 1 1 0 2 0 0 0 0 1 1
4 7 points of P* and IP-simplices
1 0 0 0 -1 0 0
0 1 0 0 -1 0 0
0 0 1 0 -1 0 0
0 0 0 1 1 -1 0
------------------------------ #IP-simp=2
1 1 1 0 1 1 5=d codim=0
0 0 0 1 0 1 2=d codim=3
\enddel The following example features all types of lattice points:
palp$ echo '16 8 4 2 1 1' | mori.x -fP
4 9 points of P* and IP-simplices
-1 0 0 2 0 0 0 1 0
-1 0 0 1 2 0 1 1 0
0 0 2 -1 1 1 1 0 0
0 1 1 0 -1 1 0 0 0
----------------------------------- #IP-simp=3
8 1 1 4 2 0 0 16=d codim=0
4 0 0 2 1 1 0 8=d codim=1
2 0 0 1 0 0 1 4=d codim=2
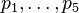 are vertices, p6,p7 further relevant points, but
p8 = − p1 = (p2 + p3 + 4p4 + 2p5) / 8 is interior to the facet spanned by
are vertices, p6,p7 further relevant points, but
p8 = − p1 = (p2 + p3 + 4p4 + 2p5) / 8 is interior to the facet spanned by
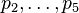 .
Note that the ordering of the CWS input is not obeyed by the output of
lattice points. Once the order is displayed, however, it
is fixed and determines the labeling of toric divisors in any further output.
.
Note that the ordering of the CWS input is not obeyed by the output of
lattice points. Once the order is displayed, however, it
is fixed and determines the labeling of toric divisors in any further output.
-K
The Kreuzer polynomial\footnote{We named this output format after Maximilian Kreuzer, who designed it. This is an example of his proverbial ability to eliminate unnecessary data redundancies and recast essential information in condensed form.} of PALP's representation of P * is displayed. It encodes lattice polytope points in a compact form. The number of variables equals the dimension of the polytope. Each lattice point gives rise to a Laurent monomial in which the exponents of the variables are the coordinates. Vertices and non-vertices are distinguished by coefficients ` + ' and ` − ' respectively. Points in the interior of facets are ignored. As this is closely connected with the way mori.x works when used without -M, the combination '-MK' is not allowed.
palp$ echo '8 4 1 1 1 1 0 6 3 1 0 1 0 1' | mori.x -fK KreuzerPoly=t_4/(t_1t_3)+t_3+t_4+t_2+t_1+t_1^3t_3^3/(t_2t_4^4); intpts=1; Pic=2
A comparison with the output for -P, which can be found here
might help for a better understanding of the present option.
Negative coordinates are always displayed by putting the variables in the denominator. The number of points in the interior of facets is shown as 'intpts'. The multiplicities of the toric divisors are displayed as 'multd' if they are greater than one. Furthermore, the Picard number of the CY hypersurface is computed and printed as 'Pic'.
-b
The zeroth and first arithmetic genera of the hypersurface are determined according to the following formulas (see F.Hirzebruch, 'Topological methods in algebraic geometry', Springer Verlag, Berlin Heidelberg New York 1995.)
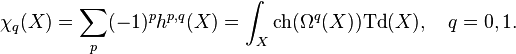
where 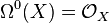 is the trivial bundle and Ω1(X) = T * X is the bundle of 1-forms, ch is the corresponding Chern character,
and Td(X) is the Todd class of X.
is the trivial bundle and Ω1(X) = T * X is the bundle of 1-forms, ch is the corresponding Chern character,
and Td(X) is the Todd class of X.
Furthermore the Euler characteristic is displayed.
Here we compute it by means of the intersection polynomial:
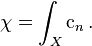 where cn is the top Chern class, n = dim X.
where cn is the top Chern class, n = dim X.
These formulas hold for arbitrary smooth hypersurfaces; in particular, they do not need to be CY.' Indeed, if X is CY, its Euler characteristic can also be computed by poly.x in terms of polytope combinatorics. Compare the two Euler characteristics for a consistency check.
Consider the K3 surface as a simple example:
palp$ echo '4 1 1 1 1' | mori.x -bf SINGULAR -> Arithmetic genera and Euler number of the CY: chi_0: 2 , chi_1: -20 [ 24 ]
As expected, the Euler characteristic is 24 and h1,1 = 20. Using the example discussed before we find
palp$ echo '8 4 1 1 1 1 0 6 3 1 0 1 0 1' | mori.x -bf SINGULAR -> Arithmetic genera and Euler number of the CY: chi_0: 0 , chi_1: 126 [ -252 ] SINGULAR -> Arithmetic genera and Euler number of the CY: chi_0: 0 , chi_1: 126 [ -252 ]
Special care is needed in the interpretation of the results for non-CY hypersurfaces: the triangulation algorithm might fail to make these varieties smooth, in which case the formulas above do not hold and hence the output is misleading; see the description of the option -H for more details.
-i
This option displays the intersection polynomial of the CY hypersurface in terms of an integral basis of the toric divisors. The coefficients of the monomials are the triple intersection numbers in this basis. This option can also be used together with -H to perform this task for non-CY hypersurfaces.
palp$ echo '8 4 1 1 1 1 0 6 3 1 0 1 0 1' | mori.x -fi SINGULAR -> divisor classes (integral basis J1 ... J2): d1=J1+3*J2, d2=J1, d3=-J1+J2, d4=J2, d5=J1, d6=J2 SINGULAR -> intersection polynomial: 2*J1*J2^2+2*J2^3 SINGULAR -> divisor classes (integral basis J1 ... J2): d1=J1+3*J2, d2=J1, d3=-J1+J2, d4=J2, d5=J1, d6=J2 SINGULAR -> intersection polynomial: 2*J1*J2^2+2*J2^3
'd1',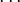 , 'd6' denote the toric divisors corresponding
to the lattice points
, 'd6' denote the toric divisors corresponding
to the lattice points 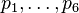 , see our standard example.
There are two independent divisor
classes. Indeed, mori.x expresses the intersection polynomial in terms
of the integral basis J1 = D2 = D5 and J2 = D4 = D6.
, see our standard example.
There are two independent divisor
classes. Indeed, mori.x expresses the intersection polynomial in terms
of the integral basis J1 = D2 = D5 and J2 = D4 = D6.
-c
The Chern classes of the hypersurface (CY or non-CY) are displayed in terms of an integral basis of the toric divisors:
palp$ echo '8 4 1 1 1 1 0 6 3 1 0 1 0 1' | mori.x -fc SINGULAR -> divisor classes (integral basis J1 ... J2): d1=J1+3*J2, d2=J1, d3=-J1+J2, d4=J2, d5=J1, d6=J2 SINGULAR -> Chern classes of the CY-hypersurface: c1(CY)= 0 c2(CY)= 10*J1*J2+12*J2^2 c3(CY)= -252 *[pt] SINGULAR -> divisor classes (integral basis J1 ... J2): d1=J1+3*J2, d2=J1, d3=-J1+J2, d4=J2, d5=J1, d6=J2 SINGULAR -> Chern classes of the CY-hypersurface: c1(CY)= 0 c2(CY)= 10*J1*J2+12*J2^2 c3(CY)= -252 *[pt]
-t
The triple intersection numbers of the toric divisors are displayed. The form of this output is designed for further use in Mathematica. The pre-compiler command 'DijkEQ' in the C file SingularInput.c controls the symbol `->' in option '-t'.
Before computing the intersection ring for our standard example, let us state some expectations.
Inspection of the data of the polytope reveals that it describes a K3
fibration with the fiber determined by the weight system 6~3~1~1~1.
There are only the two points p2,p5 outside the corresponding 3--plane,
so each of them must represent the generic fiber with self--intersection 0.
In other words, the self--intersections of d2 and d5 as well as
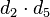 must all vanish.
This is confirmed by the following excerpt from the output:
must all vanish.
This is confirmed by the following excerpt from the output:
echo '8 4 1 1 1 1 0 6 3 1 0 1 0 1' | mori.x -ft SINGULAR -> triple intersection numbers: d6^3->2, d5*d6^2->2, d4*d6^2->2, d3*d6^2->0, d2*d6^2->2, d1*d6^2->8, d5^2*d6->0, d4*d5*d6->2, d3*d5*d6->2, d2*d5*d6->0, d1*d5*d6->6, d4^2*d6->2, d3*d4*d6->0, d2*d4*d6->2, d1*d4*d6->8, d3^2*d6->-2, d2*d3*d6->2, d1*d3*d6->2, d2^2*d6->0, d1*d2*d6->6, d1^2*d6->30, d5^3->0, d4*d5^2->0, d3*d5^2->0, d2*d5^2->0, d1*d5^2->0, d4^2*d5->2, d3*d4*d5->2, d2*d4*d5->0, d1*d4*d5->6, d3^2*d5->2, d2*d3*d5->0, d1*d3*d5->6, d2^2*d5->0, d1*d2*d5->0, d1^2*d5->18, [...]
-d
This option displays topological data of the toric divisors restricted to the (CY or non-CY) hypersurface. The Euler characteristics of the toric divisor classes and their arithmetic genera are shown.
Furthermore, in the case of a three-dimensional hypersurface, the program checks the del Pezzo property against two necessary conditions and analyses the mutual intersections of the del Pezzo candididates. The number of del Pezzo candidates is displayed followed by their type in parenthesis; furthermore, those among them that do not intersect other del Pezzo candidates are listed.
For a del Pezzo divisor S of type n, the following equations should
hold:
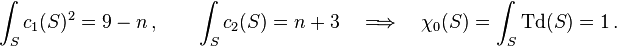 Here, 'Td(S)' denotes the Todd class of S, which gives the zeroth
arithmetic genus of S upon integration.
This test also allows to determine the type of the del Pezzo surface in
question.
A second necessary condition comes from the fact that a del Pezzo surface is a
two-dimensional Fano manifold.
Hence, the first Chern class of S integrated over all curves on S has to be
positive:
Here, 'Td(S)' denotes the Todd class of S, which gives the zeroth
arithmetic genus of S upon integration.
This test also allows to determine the type of the del Pezzo surface in
question.
A second necessary condition comes from the fact that a del Pezzo surface is a
two-dimensional Fano manifold.
Hence, the first Chern class of S integrated over all curves on S has to be
positive:
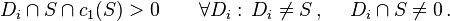 This condition would be sufficient if we were able to access all curves
of the hypersurface.
In our construction, however, we can only check for curves induced by toric
divisors. This functionality was added to carry out the analysis of base manifolds
for elliptic fibrations in arXiv:1101.4908.
This condition would be sufficient if we were able to access all curves
of the hypersurface.
In our construction, however, we can only check for curves induced by toric
divisors. This functionality was added to carry out the analysis of base manifolds
for elliptic fibrations in arXiv:1101.4908.
Consider the following example: it is well-known that the del Pezzo surface dP6 can be
realized as a homogeneous polynomial of degree 3 in 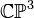 . Hence a Calabi-Yau
hypersurface in a toric variety with CWS
\begin{align}
5\,1\, 1\, 1\, 1\, 1\, 0 \nonumber\\
2\, 0\, 0\, 0\, 0\, 1\, 1 \nonumber
\end{align}
i.e. a
. Hence a Calabi-Yau
hypersurface in a toric variety with CWS
\begin{align}
5\,1\, 1\, 1\, 1\, 1\, 0 \nonumber\\
2\, 0\, 0\, 0\, 0\, 1\, 1 \nonumber
\end{align}
i.e. a 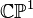 fibration over
fibration over 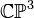 contains a dP6: setting
the last coordinate z6 to zero forces all terms to be of the form
contains a dP6: setting
the last coordinate z6 to zero forces all terms to be of the form 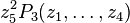 ,
where </math>P_3(z_1,\ldots ,z_4)</math> is a homogeneous polynomial of degree 3 in
,
where </math>P_3(z_1,\ldots ,z_4)</math> is a homogeneous polynomial of degree 3 in 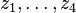 . We may set
z5 to 1 by using the second
. We may set
z5 to 1 by using the second 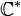 action, so that the divisor D6 corresponds to
a homogenous polynomial of degree 3 in
action, so that the divisor D6 corresponds to
a homogenous polynomial of degree 3 in 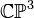 , i.e. a dP6.
, i.e. a dP6.
This is confirmed by
palp$ mori.x -d Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...': 5 1 1 1 1 1 0 2 0 0 0 0 1 1 SINGULAR -> topological quantities of the toric divisors: Euler characteristics: 46 46 46 9 46 55 Arithmetic genera: 4 4 4 1 4 5 dPs: 1 ; d4(6) nonint: 1 ; d4
Note that Palp has exchanged the ordering of the divisors, so that the dP6 is now given by D4. This divisor does not intersect any other del Pezzo as it is the only del Pezzo candidate in this example.
-a
This is a shortcut for '-gmPbictd'.
-D
An alternative way to provide the input is to type lattice polytope points of P * directly. In this case, one has to use the parameter '-D'. Let us reconsider the example of section -P:
palp$ mori.x -DP
`#lines #colums' (= `PolyDim #Points' or `#Points PolyDim'):
4 7
Type the 28 coordinates as dim=4 lines with #pts=7 columns:
1 0 0 -1 0 0 0
0 1 0 -1 0 0 0
0 0 1 -1 0 0 0
0 0 0 1 -1 1 0
4 7 points of P* and IP-simplices
1 0 0 -1 0 0 0
0 1 0 -1 0 0 0
0 0 1 -1 0 0 0
0 0 0 1 -1 1 0
------------------------------ #IP-simp=2
1 1 1 1 1 0 5=d codim=0
0 0 0 0 1 1 2=d codim=3
palp$ mori.x -DP
`#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'):
4 5
Type the 20 coordinates as dim=4 lines with #pts=5 columns:
-1 2 0 0 0
-1 1 2 0 0
0 -1 1 0 2
0 0 -1 1 1
4 9 points of P* and IP-simplices
-1 2 0 0 0 0 0 1 0
-1 1 2 0 0 0 1 1 0
0 -1 1 0 2 1 1 0 0
0 0 -1 1 1 1 0 0 0
----------------------------------- #IP-simp=3
8 4 2 1 1 0 0 16=d codim=0
4 2 1 0 0 1 0 8=d codim=1
2 1 0 0 0 0 1 4=d codim=2
Note how the order of the vertices corresponds to that of the input (cf.~section -P).
-H
Using this option, one can specify a (non-CY) hypersurface. The user determines the hypersurface divisor class
| H = | ∑ | ciDi |
| i |
in terms of the toric divisor classes Di by typing its coefficients ci. The hypersurface can then be analyzed by combining '-H' with other options, as described above. Just using '-H', the program runs '-Hb'.
The reader is warned:
smoothness is not guaranteed anymore, so that
the intersection numbers can become fractional. Some choices of the hypersurface
equation may intersect singularities not resolved by the triangulation.
Consider e.g. the hypersurface determined by the divisor class
H = D1 + D6 in our standard example.
Remember that the
order in which mori.x expects the coefficients of the hypersurface
divisor class is fixed by the polytope matrix and not by the CWS input. Hence,
the correct input for H is the string '1 0 0 0 0 1'.
palp$ mori.x -H Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' 8 4 1 1 1 1 0 6 3 1 0 1 0 1 WARNING: there is 1 facet-IP ignored in the triangulation. This may lead to unresolved singularities in the hypersurface. Type the 6 (integer) entries for the hypersurface class: 1 0 0 0 0 1 Hypersurface degrees: ( 5 4 ) Hypersurface class: 1*d1 1*d6 SINGULAR -> Arithmetic genera and Euler number of H: chi_0: 29/27 , chi_1: 128/27 [ -22/3 ]
To calculate these quantities, the program determines the characteristic classes of the divisors using adjunction. It then performs the appropriate integration with the help of the triple intersection numbers. The fractional results of the arithmetic genera and the Euler number in our example indicate that the intersection polynomial has fractional entries. This happens because the program introduces a singularity into the ambient toric variety which descends to the hypersurface H.
It is therefore much better to combine -H with -M:
palp$ mori.x -HM
Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...':
8 4 1 1 1 1 0 6 3 1 0 1 0 1
4 8
-1 0 0 0 1 3 1 0
0 0 0 1 0 -1 0 0
-1 1 0 0 0 3 1 0
1 0 1 0 0 -4 -1 0
`#triangulations':
1
1 triangulations:
12 1111000 1110010 1101010 0111001 0110011 0101011
1011100 1010110 1001110 0011101 0010111 0001111
Type the 7 (integer) entries for the hypersurface class:
1 0 0 0 0 1 0
Hypersurface degrees: ( 5 4 1 )
Hypersurface class: 1*d1 1*d6
SINGULAR -> Arithmetic genera and Euler number of H:
chi_0: 1 , chi_1: 3 [ -4 ]
As a second example, consider the quadric in 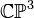 :
:
palp$ mori.x -H Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...': 4 1 1 1 1 Type the 4 (integer) entries for the hypersurface class: 2 0 0 0 Hypersurface degrees: ( 2 ) Hypersurface class: 2*d1 SINGULAR -> Arithmetic genera and Euler number of H: chi_0: 1 , chi_1: -2 [ 4 ]
The hypersurface is smooth in this case, so that the arithmetic genera and
the Euler number are those of 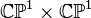 .
Of course, one needs to independently check smoothness in order to rely on
the output, as the integrality of the arithmetic genera alone is not
sufficient to conclude that the hypersurface is non-singular.
.
Of course, one needs to independently check smoothness in order to rely on
the output, as the integrality of the arithmetic genera alone is not
sufficient to conclude that the hypersurface is non-singular.
-M
Option '-M' allows polytopes of (in principle) arbitrary dimensions, but expects the triangulations to be provided by the user; it can be combined with any other option except for '-K'. As the Mori cone is analysed with PALP's routines, the parameter 'POLY\_Dmax' must possibly be adjusted for this; see the section on the parameter POLY\_Dmax.
This functionality is useful, for instance, when mori.x fails to triangulate the polytope by itself. This happens whenever the dimension of the polytope is different from four, or when the polytope contains more than three lattice points that are neither vertices nor (facet--)IPs. Fortunately, there are programs capable of efficiently performing complete triangulations of arbitrary polytopes, e.g. TOPCOM, which is also included in SAGE; the user can redirect their output as an input for mori.x to determine the Mori generators of the ambient space. Other situations where '-M' is useful arise whenever we prefer to keep control over the lattice points involved in the triangulation, rather than accept mori.x's convention of omitting precisely the interior points of facets from a completed list; this is particularly relevant if '-M' is combined with '-H'.
After the usual polytope input, P * is displayed in the following manner. If the input is of CWS type, all points of P * are given in mori.x's standard order (see section -P). If matrix input is used via '-D', the points entered by the user are displayed again in the same order, but with the origin appended (if the origin is accidentally entered somewhere in the point list, it is swapped with the last point in the list); possible further polytope points are ignored by the program, hence singularities can be introduced if desired. Then the user is asked for the number of triangulations to be analysed, and afterwards each triangulation should be entered as a line starting with the number of simplices involved in the triangulation, followed by bit sequences encoding these simplices. The number of bits in each sequence should be the number of non--zero lattice points in the displayed list, with 1's indicating that the point belongs to the simplex, and 0's otherwise.
An application to our standard example was already demonstrated in section -H. Consider also the following two-dimensional polytope:
palp$ mori.x -MDgm
`#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'):
2 7
Type the 14 coordinates as dim=2 lines with #pts=7 columns:
1 0 -1 -1 -1 -1 0
0 1 2 1 0 -1 -1
2 8
1 0 -1 -1 -1 -1 0 0
0 1 2 1 0 -1 -1 0
`#triangulations':
1
1 triangulations:
7 1100000 0110000 0011000 0001100 0000110 0000011 1000001
14 SR-ideal
0000101 0001001 0001010 0010001 0010010 0010100 0100001 0100010
0100100 0101000 1000010 1000100 1001000 1010000
6 MORI GENERATORS / dim(cone)=5
1 -2 1 0 0 0 0 I:0111011
0 1 -1 1 0 0 0 I:1101101
0 0 1 -2 1 0 0 I:1110110
0 0 0 1 -2 1 0 I:1011111
0 0 0 0 1 -1 1 I:1100011
1 0 0 0 0 1 -1 I:0111100
Since $P^*$ is just a polygon there is only one maximal triangulation of its boundary. For this reason we have typed '1' after '#triangulations'. The triangulation has seven simplices, which are just the line segments along the circumference of the polygon. For instance, the string '0011000' denotes the third simplex containing the points denoted by the third and fourth columns of the polytope matrix, i.e. the points p3 = ( − 1,2) and p4 = ( − 1,1).
As the Mori cone encodes linear relations among seven points in d = 2, it is
five-dimensional and has four-dimensional facets; there are seven of
them, as the lengths of the bit sequences after 'I:' indicate.
There are six generators.
Consider the matrix of incidences whose rows are preceded by 'I:'.
The second column reads '111011', i.e. on the second facet of the Mori
cone lie five generators.
It is easily checked that they satisfy m1 + 2m2 + m3 = m5 + m6.
All other facets contain instead four generators and are hence simplicial.