General aspects of using PALP
On this page we discuss aspects of PALP that are common to most or all of its applications. The first step is to download the package from this website and follow the compilation instructions given there, which should result in the existence of a directory `palp' containing the program as well as the executable files.
Contents |
Polytope Input
The majority of applications requires input in the form of a list of polytopes.
There are essentially two ways of entering the data of a polytope.
Matrix input starts with a line containing two numbers nlines and
ncolumns (which may be followed by text which is simply ignored
by the program) and proceeds with a matrix with the corresponding numbers
of lines and columns.
PALP requires 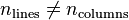 and interprets the smaller
of the two numbers as the dimension of the polytope and the other one as the
number of polytope points entered as lines or columns of input.
and interprets the smaller
of the two numbers as the dimension of the polytope and the other one as the
number of polytope points entered as lines or columns of input.
palp$ poly.x Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 3 2 This text is ignored by PALP Type the 6 coordinates as #pts=3 lines with dim=2 columns: 2 0 0 2 0 0 M:6 3 F:3 Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 2 3 The same example with transposed input Type the 6 coordinates as dim=2 lines with #pts=3 columns: 2 0 0 0 2 0 M:6 3 F:3
In both cases the input specifies the polygon (2-polytope) that is the convex
hull of the 3 points {(2,0),(0,2),(0,0)} in 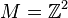 .
The output just means that this polygon has 6 lattice points, 3 vertices and 3
facets (here, edges).
The possibility of ignored text in the input is useful because PALP's output
can often be used as input for further applications; thereby extra information
can be displayed without destroying the permissible format.
.
The output just means that this polygon has 6 lattice points, 3 vertices and 3
facets (here, edges).
The possibility of ignored text in the input is useful because PALP's output
can often be used as input for further applications; thereby extra information
can be displayed without destroying the permissible format.
For applications in the context of toric geometry one should be aware of the
fact that there are two relevant, mutually dual lattices M and N whose
toric interpretations are quite different.
By default PALP interprets the input polytope as 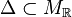 .
Note that PALP refers to this polytope as $P$; in this paper we shall
use both notations.
If Δ (=P) is reflexive, it is very natural (and, for some
applications, more natural) to consider its dual
.
Note that PALP refers to this polytope as $P$; in this paper we shall
use both notations.
If Δ (=P) is reflexive, it is very natural (and, for some
applications, more natural) to consider its dual 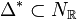 as
well.
If PALP should interpret the input as Δ * , it must be instructed to
do that by an option (`-D' for poly.x and mori.x, `-N' for nef.x).
In fact, in the case of mori.x it would be extremely unnatural to use
Δ as input; therefore matrix input is allowed only with `-D' to
avoid errors.
as
well.
If PALP should interpret the input as Δ * , it must be instructed to
do that by an option (`-D' for poly.x and mori.x, `-N' for nef.x).
In fact, in the case of mori.x it would be extremely unnatural to use
Δ as input; therefore matrix input is allowed only with `-D' to
avoid errors.
A second input format uses the fact that many polytopes (in particular the ones
related to the toric description of weighted projective spaces) afford a
description as the convex hull of all points X that lie in the
(n − 1)-dimensional sublattice
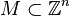 determined by
determined by 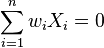 and satisfy the
inequalities
and satisfy the
inequalities 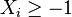 for
for 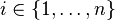 .
Given such a weight system in the format d w1 w2 ... wn where the wi
must be positive integers and
.
Given such a weight system in the format d w1 w2 ... wn where the wi
must be positive integers and
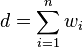 , PALP computes the corresponding list of points and
makes a transformation to
, PALP computes the corresponding list of points and
makes a transformation to 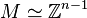 .
The following example corresponds to the Newton polytope of the quintic
threefold in
.
The following example corresponds to the Newton polytope of the quintic
threefold in 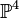 .
.
palp$ poly.x -v Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 5 1 1 1 1 1 4 5 Vertices of P -1 4 -1 -1 -1 -1 -1 4 -1 -1 -1 -1 -1 4 -1 -1 -1 -1 -1 4
As the first line of the prompt indicates, this format can be generalized
to the case
of k weight systems describing a polytope in 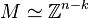 .
We call the corresponding data, which should satisfy
.
We call the corresponding data, which should satisfy
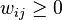 and
and 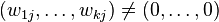 ,
a CWS ('combined weight system').
,
a CWS ('combined weight system').
It is also possible to specify a sublattice of finite index corresponding to
the condition 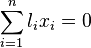 mod r by writing /Zr: l1 ...ln
after the specification of the (C)WS.
mod r by writing /Zr: l1 ...ln
after the specification of the (C)WS.
In the following example, 21100 20011 describes a square whose edges
have lattice length 2, whereas the condition indicated by Z2: 1 0 1 0
eliminates the interior points of the edges.
The particular output arises because PALP transforms the original and
the reduced lattice to 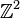 in different ways.
in different ways.
palp$ poly.x -v
Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...'
or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'):
2 1 1 0 0 2 0 0 1 1
2 4 Vertices of P
-1 1 -1 1
-1 -1 1 1
Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...'
or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'):
2 1 1 0 0 2 0 0 1 1 /Z2: 1 0 1 0
2 4 Vertices of P
-1 0 0 1
1 -1 1 -1
For a reconstruction of the CWS given a polytope as matrix input see the option cws.x -N.
If PALP is used interactively, it can be terminated by entering an empty line instead of the data of a polytope. In the case of file input the end of the file results in the termination.
Error Handling
PALP is designed in such a way that it should exit with an error message rather than crash or display wrong results. The main sources for problems are inappropriately set parameters, lack of memory and numerical overflows. The most important settings of parameters all occur at the beginning of Global.h, which is probably the only file that a user may want to modify.
Here are some typical error messages.
If we want to analyze the Calabi-Yau sixfold that is a
hypersurface in 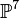 with poly.x, the following will happen
if PALP has been compiled with the default settings.
with poly.x, the following will happen
if PALP has been compiled with the default settings.
8 1 1 1 1 1 1 1 1 Please increase POLY_Dmax to at least 7
In this case one should edit Global.h (see also section Polydmax), setting
#define POLY_Dmax 7 /* max dim of polytope */
and compile again. Similarly the program may ask for changes of other basic parameters, all of which are defined within the first 52 lines of Global.h.
In many cases we have implemented checks with the help of the `assert' routine, leading to error messages such as the following.
poly.x: Vertex.c:613: int Finish_IP_Check(PolyPointList *, ... EqList *, CEqList *, INCI *, INCI *): Assertion `_V->nv<32' failed. Abort
In this case one should look up line 613 of Vertex.c,
assert(_V->nv<VERT_Nmax);
This indicates that the value of _V->nv has risen above the value 32 assigned to VERT_Nmax in Global.h and that the value of VERT_Nmax should be changed correspondingly. At this point it is important to note that the setting of parameters in Global.h depends on the setting of POLY_Dmax:
#define POLY_Dmax 6 /* max dim of polytope */ ... #if (POLY_Dmax <= 3) #define POINT_Nmax 40 /* max number of points */ #define VERT_Nmax 16 /* max number of vertices */ #define FACE_Nmax 30 /* max number of faces */ #define SYM_Nmax 88 /* cube: 2^D*D! plus extra */ #elif (POLY_Dmax == 4) #define POINT_Nmax 700 /* max number of points */ #define VERT_Nmax 64 /* max number of vertices */ ...
Of course one should then modify a parameter such as VERT_Nmax or SYM_Nmax at the position corresponding to the chosen value of POLY_Dmax. For POLY_Dmax taking values up to 4, the default parameters in Global.h are chosen in such a way that they work for any reflexive polytope.
While the error messages mentioned above are related to parameter values that are too low, excessively high values may also lead to problems such as slowing down the calculation. In particular, computation time depends very sensitively upon whether VERT_Nmax is larger than 64. Very high parameter values may also lead to troubles with memory which manifest themselves in error messages such as Unable to alloc space for ... or Allocation failure in ... or even Segmentation fault. In such a case one can only check whether there are possibilities for making parameters smaller, or use a computer with more RAM.
An assertion failure that
does not refer to an inequality involving a parameter or an allocation
failure, such as
NFX_Limit in GL -> 1074575416 !!
is very likely to point to a numerical overflow. In such a case it might help to change line 12 of Global.h from
#define Long long
to
#define Long long long
These issues are particularly relevant to the analysis of high-dimensional polytopes, e.g. in the case of nef.x with nef partitions of large length. In this case, it may happen that certain parameters in the header file Nef.h may need to be modified. Here we give a particularly nasty example:
palp$ nef.x -Lp -N -c6 -P Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 7 9 Please increase POLY_Dmax to at least 12 = 7 + 6 - 1 (nef.x requires POLY_Dmax >= dim N + codim - 1)
This means that in Global.h we need to set POLY_Dmax to at least 12:
#define POLY_Dmax 12 /* max dim of polytope */
After recompiling PALP we get further but not far enough:
palp$ nef.x -Lp -N -c6 -P
Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...'
or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'):
7 9
Type the 63 coordinates as dim=7 lines with #pts=9 columns:
1 0 0 0 0 -1 0 0 -1
0 1 0 0 0 -1 0 0 -1
0 0 1 0 0 -1 0 0 -1
0 0 0 1 0 -1 0 0 0
0 0 0 0 1 -1 0 0 0
0 0 0 0 0 0 1 0 -1
0 0 0 0 0 0 0 1 -1
M:5214 12 N:10 9 codim=6 #part=1
7 10 Points of Poly in N-Lattice:
1 0 0 0 0 -1 0 0 -1 0
0 1 0 0 0 -1 0 0 -1 0
0 0 1 0 0 -1 0 0 -1 0
0 0 0 1 0 -1 0 0 0 0
0 0 0 0 1 -1 0 0 0 0
0 0 0 0 0 0 1 0 -1 0
0 0 0 0 0 0 0 1 -1 0
--------------------------------------------------
1 1 1 1 1 1 0 0 0 d=6 codim=2
1 1 1 0 0 0 1 1 1 d=6 codim=2
nef.x: Vertex.c:613: Finish_Find_Equations:
Assertion `_V->nv<64' failed.
Aborted
This can be remedied by adjusting the global variable VERT_Nmax in Global.h as follows (it should not be too large):
#define VERT_Nmax 128 /* !! use optimal value !! */
After recompilation it works for a while. Then the following error occurs
Unable to alloc space for _BL
This means that the program has run out of memory.
Some Peculiarities of PALP
Much of PALP's code was written originally with a very specific aim (the classification problem) in mind, and not with the intention of designing a package that would be immediately accessible to many users. Other applications were added later by different people. This has resulted in several peculiar features whose comprehension might help to avoid errors. In the following we list a few of them.
Option names
PALP does not have any clear convention on how options are named. In fact, it can happen that options with the same effects have different names in different parts of the package: for instance, in order to make PALP interpret an input polytope as the (dual) N lattice polytope, one has to use `-D' with poly.x and mori.x but `-N' with nef.x. Ironically, poly.x also has an option `-N' whose effect is completely different.
It is also worth noting that poly.x and mori.x admit concatenating several options into one string, e.g. poly.x -gve, mori.x -Hb whereas other programs require them to be separate, e.g. nef.x -Lp -N -c6 -P.
Indexing Conventions
Most of PALP, being programmed in C, follows the convention of using
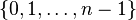 as the standard n element set.
So lists of vertices take the form
as the standard n element set.
So lists of vertices take the form 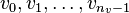 , a list
of points is given as
, a list
of points is given as 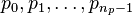 , and so on.
The exception is mori.x which uses
, and so on.
The exception is mori.x which uses 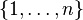 as the standard set.
as the standard set.
Binary representation of incidences
PALP represents incidences as bit patterns both internally and in its output;
in the case of mori.x -M even input is required in that format.
This works in the following manner.
To any face ϕ and vertex vi of P a bit bi
is assigned via bi = 1 if 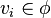 and bi = 0 otherwise;
and bi = 0 otherwise;
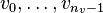 are ordered as in the output of poly.x -v.
This results in a bit pattern Bv(ϕ) which
can be written as if it represented a binary number,
are ordered as in the output of poly.x -v.
This results in a bit pattern Bv(ϕ) which
can be written as if it represented a binary number,
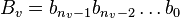 .
This is the convention implemented in poly.x, whereas mori.x writes it as a
sequence from left to right,
.
This is the convention implemented in poly.x, whereas mori.x writes it as a
sequence from left to right, 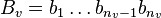 (remember the
last entry about indexing conventions!).
Furthermore, a bit pattern
(remember the
last entry about indexing conventions!).
Furthermore, a bit pattern 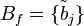 related to P's facets
fj (ordered as in the output of poly.x -e) can be assigned via
related to P's facets
fj (ordered as in the output of poly.x -e) can be assigned via
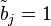 if
if 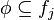 and
and 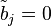 otherwise.
otherwise.
The parameter POLY_Dmax
POLY_Dmax (line 22 of Global.h) is the most important parameter to set before compilation; for most applications it is probably the only parameter one has to care about. Since palp-2.11, it is possible to set POLY_Dmax without editing Global.h. For example, as a linux user who wants to change POLY_Dmax to 4, you can do the following.
palp-2.11$ make cleanall palp-2.11$ export CPPFLAGS=-DPOLY_Dmax=4 palp-2.11$ make
While it usually suffices to have POLY_Dmax not smaller than the dimension of any polytope that one wants to analyze, there are the following important exceptions:
- nef.x normally requires POLY_Dmax
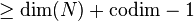 , which is the dimension of the support polytope of the corresponding Gorenstein cone which nef.x analyzes;
, which is the dimension of the support polytope of the corresponding Gorenstein cone which nef.x analyzes;
- nef.x -G requires POLY_Dmax
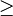 dim(input-polytope) +1 because the input-polytope is interpreted as the support of the cone and the full dimension of the cone is required for technical reasons;
dim(input-polytope) +1 because the input-polytope is interpreted as the support of the cone and the full dimension of the cone is required for technical reasons;
- mori.x -MD requires POLY_Dmax
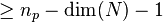 , the dimension of the Mori cone; np is the total number of input points including the lattice origin, hence the subtraction of 1.
, the dimension of the Mori cone; np is the total number of input points including the lattice origin, hence the subtraction of 1.
IP property and IP simplices
In PALP's help screens and output messages every now and then the abbreviation IP occurs. A priori this is just a shortcut for writing `interior point', as in `the generic CY hypersurface does not intersect the divisors corresponding to IPs of facets'. However, when we say that a polytope has the IP property, we mean that the polytope has the lattice origin in its interior. IP simplices are simplices with this property, usually with vertices that are points or vertices of some given polytope. This concept played an important role in the classification scheme of hep-th/9512204, alg-geom/9603007, math/0001106. The lattice vectors corresponding to the vertices of an IP simplex define a linear relation with positive coefficients which is unique up to scaling. Conversely any positive linear relation among lattice points that cannot be written as the sum of two other such relations defines an IP simplex. Of course, the set of coefficients is just the weight system defined by the IP simplex.