Documentation on poly.x
poly.x is the program that provides an interface for PALP's general purpose routines as well as certain specialized applications that do not belong to any of the other executables. In other words, poly.x deals with all applications that are not related to nef partitions, Mori cones or the classification of reflexive polytopes.
Help Screen
As for all of PALP's programs, a rough guide can be obtained with the help option:
palp$ poly.x -h
This is 'poly.x': computing data of a polytope P
Usage: poly.x [-<Option-string>] [in-file [out-file]]
Options (concatenate any number of them into <Option-string>):
h print this information
f use as filter
g general output:
P reflexive: numbers of (dual) points/vertices, Hodge numbers
P not reflexive: numbers of points, vertices, equations
p points of P
v vertices of P
e equations of P/vertices of P-dual
m pairing matrix between vertices and equations
d points of P-dual (only if P reflexive)
a all of the above except h,f
l LG-`Hodge numbers' from single weight input
r ignore non-reflexive input
o ignore non-IP input
q quick version of og, incompatible with other options
D dual polytope as input (ref only)
n do not complete polytope or calculate Hodge numbers
i incidence information
s check for span property (only if P from CWS)
I check for IP property
S number of symmetries
T upper triangular form
N normal form
t traced normal form computation
V IP simplices among vertices of P*
P IP simplices among points of P* (with 1<=codim<=# when # is set)
Z lattice quotients for IP simplices
# #=1,2,3 fibers spanned by IP simplices with codim<=#
## ##=11,22,33,(12,23): all (fibered) fibers with specified codim(s)
when combined: ### = (##)#
A affine normal form
B Barycenter and lattice volume [# ... points at deg #]
F print all facets
G Gorenstein: divisible by I>1
L like 'l' with Hodge data for twisted sectors
U simplicial facets in N-lattice
U1 Fano (simplicial and unimodular facets in N-lattice)
U5 5d fano from reflexive 4d projections (M lattice)
C1 conifold CY (unimodular or square 2-faces)
C2 conifold FANO (divisible by 2 & basic 2 faces)
E symmetries related to Einstein-Kaehler Metrics
Input: degrees and weights `d1 w11 w12 ... d2 w21 w22 ...'
or `d np' or `np d' (d=Dimension, np=#[points]) and
(after newline) np*d coordinates
Output: as specified by options
If an input file is indicated, "poly.x" reads its input data from there; otherwise it asks for input interactively. The output is displayed to the screen unless an output file is specified. The following subsection will explain all of the possible options, in the order in which they appear in the help screen. Here is a rough guide in terms of specific topics:
- General polytope analysis without reference to toric geometry or string theory: -g, -p, -v, -e, -m, -d, -a, -i, -s, -I, -T, -N, -t, -A, -B, -F, -G, -U, -U1, -E;
- Conifold singularities: -C1, -C2;
- Fano varieties: -U1, -U5, -C2;
- Fibration structures: -[number], -V, -P, -Z;
- IP property (see section IP Property and IP simplices): -I;
- IP simplices (see section IP Property and IP simplices): -V, -P, -Z, -[number];
- Landau-Ginzburg type superconformal field theories: -l, -L;
- Normal forms: -N, -A;
- Sublattices and quotient actions: -S, -Z, -G;
- Symmetries of a polytope: -S, -t.
Options of poly.x
As many of the following options are very simple to use, we do not always provide examples. In such cases we highly recommend to simply try using the option with simple input, e.g. the weight system "5 1 1 1 1 1" corresponding to the quintic, and a simple non-reflexive example such as
3 2 Type the 6 coordinates as #pts=3 lines with dim=2 columns: 2 0 0 2 0 0
no option set
In this case the program behaves as if the `-g' option (see below) were set. This is also the case if no option other than `-r', `-D', `-n', `-Z', `-U' or `-U1', which do not generate any output per se, is applied.
-h
The help screen is displayed (see above).
-f
The filter flag switches off the prompt for input data. This is useful for building pipelines.
-g
The following output is generated.
First, the input is repeated if it is of weight/CWS type,
but not otherwise.
Then the numbers 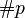 and
and 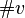 of lattice points and vertices,
respectively, are displayed in the format `M:
of lattice points and vertices,
respectively, are displayed in the format `M: 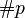
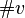 '.
The remaining output depends on whether P is reflexive.
In this case the numbers
'.
The remaining output depends on whether P is reflexive.
In this case the numbers 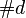 and
and 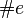 of dual lattice points
and vertices are displayed in the format `N:
of dual lattice points
and vertices are displayed in the format `N: 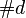
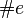 ',
followed by information on the Hodge numbers of the corresponding
Calabi--Yau manifold if dim
',
followed by information on the Hodge numbers of the corresponding
Calabi--Yau manifold if dim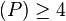 ;
in the case of a three dimensional polytope corresponding to a K3
surface, where the Hodge numbers are determined anyway, information on
the Picard number and the `correction term' is given instead
(the latter is the non-linear term in
Batyrev's formula for the Picard number alg-geom/9310003;
the Picard numbers of a K3 and its mirror add up to 20 + Cor).
For non-reflexive P the number
;
in the case of a three dimensional polytope corresponding to a K3
surface, where the Hodge numbers are determined anyway, information on
the Picard number and the `correction term' is given instead
(the latter is the non-linear term in
Batyrev's formula for the Picard number alg-geom/9310003;
the Picard numbers of a K3 and its mirror add up to 20 + Cor).
For non-reflexive P the number 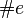 of facets is shown as `F:
of facets is shown as `F: 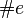 '.
'.
Using this option implies the completion of the set of lattice points in the convex hull (`points' in the help screen always means `lattice points'). In the reflexive case it also leads to the completion of the dual polytope and the computation of the complete incidence structure which is required for the calculation of the Hodge numbers. For large dimensions (say, beyond 9) these tasks may result in a long response time or in a crash of the program. In such a case one should use other options, e.g. "-nve" if information on the number of lattice points or Hodge numbers is not required.
-p
The lattice points of the polytope are displayed.
-v
The vertices of the polytope are displayed.
-e
The equations of the hyperplanes bounding the polytope are displayed.
If the polytope is not reflexive, these facet equations are given as lines
`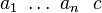 ' normalized
such that the ai have no common divisor and the
inequalities
' normalized
such that the ai have no common divisor and the
inequalities 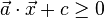 are satisfied for all points of P.
are satisfied for all points of P.
Reflexivity of a lattice polytope P is equivalent to P * being a
lattice polytope, i.e. to c = 1 for all facet equations. In that situation
the lines 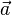 can be interpreted as vertices of P * and
"poly.x" omits the final column of 1's, indicating that the resulting matrix
can be interpreted as the list of vertices of the dual polytope.
This has the advantage that the output can be used as input for further
computations.
can be interpreted as vertices of P * and
"poly.x" omits the final column of 1's, indicating that the resulting matrix
can be interpreted as the list of vertices of the dual polytope.
This has the advantage that the output can be used as input for further
computations.
palp$ poly.x -e Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 3 2 Type the 6 coordinates as #pts=3 lines with dim=2 columns: 1 0 0 1 0 0 3 2 Equations of P 1 0 0 0 1 0 -1 -1 1 Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 3 2 Type the 6 coordinates as #pts=3 lines with dim=2 columns: 1 0 0 1 -1 -1 3 2 Vertices of P-dual <-> Equations of P 2 -1 -1 2 -1 -1
In the first case the output indicates that P can be described by
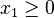 ,
, 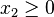 ,
, 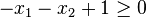 ; in the second case, where a last
output column of 1's only is implicit, P corresponds to
; in the second case, where a last
output column of 1's only is implicit, P corresponds to
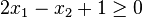 ,
, 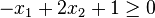 ,
, 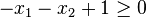 .
.
-m
One gets the 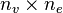 matrix with entries
matrix with entries
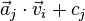 ,
, 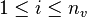 ,
, 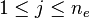 , where
nv, ne are the numbers of vertices and equations, respectively.
The elements of this `pairing matrix'
represent the lattice distances between the respective vertices and
facets.
The orders of vertices and facets are the same as for `-v' and `-e',
so it is useful to combine `-m' with these options to see precisely
which vertex and facet an entry of the pairing matrix corresponds to.
, where
nv, ne are the numbers of vertices and equations, respectively.
The elements of this `pairing matrix'
represent the lattice distances between the respective vertices and
facets.
The orders of vertices and facets are the same as for `-v' and `-e',
so it is useful to combine `-m' with these options to see precisely
which vertex and facet an entry of the pairing matrix corresponds to.
-d
If the polytope is reflexive the lattice points of the dual polytope are displayed.
-a
This is a shortcut for `-gpvemd'; it can be combined with any other options.
-l
This option is relevant to applications in the context of Landau-Ginzburg
models.
Together with its close relative `-L', it is the only option of "poly.x" that
requires non-standard input.
Rather than indicate a polytope via matrix or CWS input, one specifies
a single weight system which need not satisfy 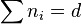 , which is interpreted as data for a superconformal field theory.
If the central charge of this SCFT is a multiple of 3 (which is required by
PALP 2.1), the analogue of the Hodge numbers is computed, see Vafa, Cumrun, "String Vacua and Orbifoldized L-G Models", Mod.Phys.Lett. A4 1169 and Intriligator, Kenneth A. and Vafa, Cumrun, "LANDAU-GINZBURG ORBIFOLDS" Nucl.Phys. B339, 95-120
, which is interpreted as data for a superconformal field theory.
If the central charge of this SCFT is a multiple of 3 (which is required by
PALP 2.1), the analogue of the Hodge numbers is computed, see Vafa, Cumrun, "String Vacua and Orbifoldized L-G Models", Mod.Phys.Lett. A4 1169 and Intriligator, Kenneth A. and Vafa, Cumrun, "LANDAU-GINZBURG ORBIFOLDS" Nucl.Phys. B339, 95-120
palp$ poly.x -l type degree and weights [d w1 w2 ...]: 5 1 1 1 1 1 5 1 1 1 1 1 M:126 5 N:6 5 V:1,101 [-200] type degree and weights [d w1 w2 ...]: 3 1 1 1 1 1 1 3 1 1 1 1 1 1 M:56 6 F:6 LG: H0:1,0,1 H1:0,20 H2:1 RefI2 type degree and weights [d w1 w2 ...]: 3 1 1 1 1 1 1 /Z3: 0 1 2 0 1 2 3 1 1 1 1 1 1 /Z3: 0 1 2 0 1 2 M:20 6 F:6 LG: H0:1,0,1 H1:0,20 H2:1 RefI2
Here the first example is the familiar quintic treated as the Gepner model (3)5, the second example is the Gepner model (1)6 and the third example an orbifold of the second one. More information can be found in section 4.1 of math/0204356.
-r
Any input that does not correspond to a reflexive polytope will be ignored. This is useful for filtering out reflexive polytopes from a larger list and saves calculation time if one is interested only in reflexive polytopes.
-o
Any input that does not result in a polytope with the IP property is simply ignored. This is useful, for example, in higher-dimensional classification problems, where not only reflexive but also other IP weight systems play a role whereas non-IP weight systems are to be discarded.
-q
This option produces the same output as -og, but is considerably faster, particularly for dimensions > 4. It cannot be combined with other options, however.
-D
The input is regarded as the dual polytope 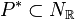 .
As this makes sense only in the reflexive case there is an error
message (but no exit from the program) for non-reflexive input.
This option is useful, in particular, if one wants to have
control over the order of the points in the N lattice.
.
As this makes sense only in the reflexive case there is an error
message (but no exit from the program) for non-reflexive input.
This option is useful, in particular, if one wants to have
control over the order of the points in the N lattice.
-n
The completion of the set of lattice points is suppressed. Hence the Hodge numbers cannot be calculated and the output will look like the one for non-reflexive polytopes even in the reflexive case. In particular, if the input is not of the (C)WS type, the number of points may be displayed wrongly. If dim(M) is large this option saves a lot of calculation time.
-i
Information on the incidence structure is displayed in the following manner. Remember from section Binary representation of incidences that any face ϕ can be assigned a bit pattern Bv(ϕ) encoding which vertices lie on ϕ and a bit pattern Bf(ϕ) encoding to which facets ϕ belongs. " poly.x -i" displays both types of bit patterns as binary numbers for all faces of P, with ` v[i]:' starting a line of Bv's corresponding to i-faces and ` f[j]:' starting a line of Bf's corresponding to j-faces. Bit patterns at the same positions in the `v[i]:' and `f[i]:' lines correspond to the same i-faces. The orders of faces within the lines are a consequence of the way PALP computes them; they conform to other output of other options in the case of i = n − 1 (facets) but not for i = 0 (vertices).
-s
This option refers to a property of (combined) weight systems that was
considered in the early stages of the classification program
hep-th/9512204.
In the higher dimensional embedding defined by a
weight system, the polytope is bounded by the inequalities 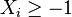 .
We say that the polytope has the span property if the pullbacks of
the equations Xi = − 1 to the subspace carrying the polytope are spanned by
vertices of the polytope, i.e. if these equations correspond to
facets.
With `-s' a message is given if the (combined) weight systems does
not have this property (try, for example, the weight system `8 3 3 2').
.
We say that the polytope has the span property if the pullbacks of
the equations Xi = − 1 to the subspace carrying the polytope are spanned by
vertices of the polytope, i.e. if these equations correspond to
facets.
With `-s' a message is given if the (combined) weight systems does
not have this property (try, for example, the weight system `8 3 3 2').
-I
There is a message if the polytope does not have the origin of the coordinate system in its interior.
-S
The output contains the following two numbers.
The first is the number of lattice automorphisms (elements of
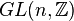 ) that leave the polytope invariant;
each such automorphism acts as a permutation on the set of vertices.
The second one is the number of permutations of the set of vertices
that leave the vertex pairing matrix (see section -m) invariant
(after taking into account the induced permutations of facets).
This number can also be interpreted as the number of symmetries of
the polytope in
) that leave the polytope invariant;
each such automorphism acts as a permutation on the set of vertices.
The second one is the number of permutations of the set of vertices
that leave the vertex pairing matrix (see section -m) invariant
(after taking into account the induced permutations of facets).
This number can also be interpreted as the number of symmetries of
the polytope in 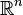 ; it may be larger than the
number of symmetries in the given lattice.
; it may be larger than the
number of symmetries in the given lattice.
palp$ poly.x -S Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 5 1 1 1 1 1 #GL(Z,4)-Symmetries=120, #VPM-Symmetries=120 Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 5 1 1 1 1 1 /Z5: 0 1 2 3 4 #GL(Z,4)-Symmetries=20, #VPM-Symmetries=120
In the first case the symmetry group of the lattice polytope and that of the
vertex pairing matrix are just the permutation group of the 5 vertices,
of order 120.
In the second case the invariance under the 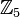 group fixes any
permutation once the permutations of two of the five vertices have been chosen,
reducing the number of group elements to 20.
The vertex pairing matrix remains the same, namely diag(5, 5, 5, 5, 5), and
therefore keeps all 120 symmetries.
group fixes any
permutation once the permutations of two of the five vertices have been chosen,
reducing the number of group elements to 20.
The vertex pairing matrix remains the same, namely diag(5, 5, 5, 5, 5), and
therefore keeps all 120 symmetries.
-T
A coordinate change is performed that makes the matrix of coordinates of the points specified in the input upper triangular, with minimal entries above the diagonal. This may be useful for representing the polytope in a specific lattice basis consisting of points of P, or for finding the volume of a specific cone (if the generators of the cone are the first input points, the volume will be the product of the entries in the diagonal after the transformation). Using this option only makes sense if its results are displayed. Therefore it exits with an error if it is not combined with an output generating option (`-v' is a natural choice).
-N
This option leads to the computation of a normal form of the polytope, i.e. a matrix containing the vertices in a specific order in a particular coordinate system, such that this output is the same for any two polytopes related by a lattice automorphism (see section 3.4 of hep-th/9805190 for the actual algorithm). This is useful, for example, if two polytopes are suspected to be isomorphic because they are isomorphic if and only if their normal forms are identical.
Example: the weight systems `3402 40 41 486 1134 1701' and `3486 41 42 498 1162 1743' give rise to the same pair of Hodge numbers (491, 11). The suspicion that they correspond to the same polytope is confirmed by
palp$ poly.x -N Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 3402 40 41 486 1134 1701 4 5 Normal form of vertices of P perm=43210 1 0 0 0 -42 0 1 0 0 -28 0 0 1 0 -12 0 0 0 1 -1 Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 3486 41 42 498 1162 1743 4 5 Normal form of vertices of P perm=43210 1 0 0 0 -42 0 1 0 0 -28 0 0 1 0 -12 0 0 0 1 -1
The perm=... part indicates how the vertices of the polytope had to be permuted to arrive at the normal form; this is only interesting if the input is of matrix type.
-t
The calculation of the normal form involves determining the pairing matrix, a normal form for the pairing matrix, an analysis of which symmetries leave this normal form invariant, a preferred ordering of the vertices and a conversion of the resulting vertex coordinate matrix to upper triangular form. The results of these steps, which may provide further useful information on the structure of P, are displayed.
-V
The IP simplices (see section IP Property and IP simplices) whose vertices are also vertices of the dual polytope are displayed. For illustrating examples look at the next options (`-P', `-Z') which are closely related.
-P
The IP simplices (see section IP Property and IP simplices) whose vertices are lattice points of the dual polytope P * are displayed. This option should only be used if it is fairly clear that P * does not have too many lattice points.
palp$ poly.x -P
Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...'
or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'):
6 1 2 3
2 7 points of P-dual and IP-simplices
1 0 -2 -1 0 -1 0
0 1 -3 -2 -1 -1 0
------------------------------ #IP-simp=4
2 3 1 0 0 0 6=d codim=0
1 2 0 1 0 0 4=d codim=0
1 1 0 0 0 1 3=d codim=0
0 1 0 0 1 0 2=d codim=1
This example shows that the N lattice polytope for 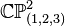 contains
3 lattice triangles with the origin in their respective interiors, as well
as a lattice line segment with that property.
The weight systems corresponding to these simplices are indicated.
contains
3 lattice triangles with the origin in their respective interiors, as well
as a lattice line segment with that property.
The weight systems corresponding to these simplices are indicated.
-Z
This option only has an effect if combined with V or P.
Any IP simplex S of dimension d occurring there defines two potentially
distinct d dimensional sublattices of N:
the lattice generated by the vertices of S,
and the sublattice of N lying in the linear subspace that is spanned by S.
Then the program computes the corresponding quotient action.
The following example illustrates this for the case of a bipyramid over a
triangle whose vertices generate an index 3 sublattice of 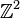 .
.
palp$ poly.x -VZD
Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...'
or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'):
3 5
Type the 15 coordinates as dim=3 lines with #pts=5 columns:
-1 -1 2 0 0
-1 2 -1 0 0
0 0 0 1 -1
3 5 vertices of P-dual and IP-simplices
-1 -1 2 0 0
-1 2 -1 0 0
0 0 0 1 -1
------------------------- #IP-simp=2 I=3 /Z3: 2 1 0 0 0
1 1 1 0 0 3=d codim=1 /Z3: 2 1 0 0 0
0 0 0 1 1 2=d codim=2
-[numbers]
If one of the options `-B', `-U' or `-C' is set, any number is assumed to
refer to that option (see below for descriptions).
Otherwise information on fibration structures of the Calabi--Yau manifold
corresponding to a reflexive polytope is displayed.
These structures correspond to reflexive subpolytopes of the N
lattice polytope P * that are intersections of the dual polytope with a
linear subspace of 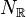 ; see, e.g.,
hep-th/9610154,hep-th/9701175 and math/0001106.
As this is a time consuming task and the desired output format may vary, there exist two different versions.
; see, e.g.,
hep-th/9610154,hep-th/9701175 and math/0001106.
As this is a time consuming task and the desired output format may vary, there exist two different versions.
If a single number 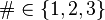 is specified, the intersections of
P * with all linear subspaces spanned by IP simplices (see section
IP Property and IP simplices) are checked for reflexivity.
This is much faster than a complete search for fibration structure but
misses fibrations whose corresponding subspaces are only spanned
by a combination of two or more IP simplices.
The codimension of the IP simplices is restricted to
is specified, the intersections of
P * with all linear subspaces spanned by IP simplices (see section
IP Property and IP simplices) are checked for reflexivity.
This is much faster than a complete search for fibration structure but
misses fibrations whose corresponding subspaces are only spanned
by a combination of two or more IP simplices.
The codimension of the IP simplices is restricted to
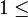 codim
codim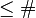 (in contrast to our usual policy this option has a
side effect on `-P' if combined with that option).
The output has the same structure as that of nef -F*.
(in contrast to our usual policy this option has a
side effect on `-P' if combined with that option).
The output has the same structure as that of nef -F*.
If two numbers are specified, all fibration structures of the given type are computed. For `-11', `-22' and `-33' all reflexive sections of codimension 1, 2 and 3, respectively, are constructed. For `-12' and `-23' all reflexive subpolytopes of codimension 1 and 2 that themselves contain a reflexive subpolytope with relative codimension 1 are constructed. The output is a polytope in the N lattice whose choice of bases and whose order of points reflects the fibration structure. For example, CY threefolds that are both K3 and elliptically fibered are found by applying " poly.x -12" to reflexive 4-polytopes, and fourfolds of that type are found by applying " poly.x -23" to reflexive 5-polytopes.
palp$ poly.x -12 Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 84 1 1 12 28 42 4 25 Em:7 3 n:7 3 Km:24 4 n:24 4 M:680 5 N:26 5 p=13bgjn256789... 1 0 -2 -1 0 -1 0 -14 -12 -10 -8 -6 -4 -9 -7 -5 -3 -4 -2 -7 -5 ... 0 1 -3 -2 -1 -1 0 -21 -18 -15 -12 -9 -6 -14 -11 -8 -5 -7 -4 -10... 0 0 0 0 0 0 1 -6 -5 -4 -3 -2 -1 -4 -3 -2 -1 -2 -1 -3 -2 -1 ... 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
Here " Em:7 3 n:7 3" refers to data of the elliptic fiber E lying within the K3 fiber indicated by " Km:24 4 n:24 4". The 25 non-zero points of the N lattice polytope are displayed in an order (first points from the subspace corresponding to E, then points in the K3 but not in E, finally all other points) and a coordinate system (only the first 2 coordinates non-vanishing for E, last coordinate vanishing for the K3) that reflect the corresponding nesting of polytopes. The sequence after p= indicates what permutation with respect to the original order of these points led to this representation (this is only interesting if the points were entered directly with the `-D' option). Further examples on how to use the fibration options can be found in section 4.2 of math/0204356.
-A
Given an arbitrary lattice polytope P, " poly.x -A"
computes its `affine normal form', i.e. a polytope in 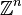 affinely isomorphic to P, such that the normal forms of two polytopes P and Q
coincide if and only if P and Q are related by an affine lattice
isomorphism
(cf. `-N', which performs the same task w.r.t. linear rather than affine
transformations).
affinely isomorphic to P, such that the normal forms of two polytopes P and Q
coincide if and only if P and Q are related by an affine lattice
isomorphism
(cf. `-N', which performs the same task w.r.t. linear rather than affine
transformations).
-B
For a given polytope its volume (normalized such that the standard simplex has volume 1) and the coordinates of its barycentre are displayed.
If an integer n is specified after `-B', the polytope is interpreted as the
origin and the first level of a Gorenstein cone. The points of the cone up to
level n are computed and displayed together with information on the type
of face of the cone they represent (w.r.t. codimension, i.e. the origin has maximal codimension and points interior to the cone have cd=0).
As example, we consider the Gorenstein cone with support
polytope given by the dual of the Newton polytope of the quintic hypersurface in 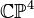
palp$ poly.x -B2 Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 5 6 Type the 30 coordinates as dim=5 lines with #pts=6 columns: 1 1 1 1 1 0 1 0 0 0 -1 0 0 1 0 0 -1 0 0 0 1 0 -1 0 0 0 0 1 -1 0 vol=5, baricent=(5,0,0,0,0)/6 IPs: 2 -2 -2 -2 -2 cd=4 2 -1 -1 -1 0 cd=3 2 0 0 0 2 cd=4 2 -1 0 -1 -1 cd=3 2 0 1 0 1 cd=3 2 0 2 0 0 cd=4 2 -1 -1 0 -1 cd=3 2 0 0 1 1 cd=3 2 0 1 1 0 cd=3 2 0 0 2 0 cd=4 2 -1 -1 -1 -1 cd=0 2 0 0 0 1 cd=0 2 0 1 0 0 cd=0 2 0 0 1 0 cd=0 2 0 0 0 0 cd=0 2 0 -1 -1 -1 cd=3 2 1 0 0 1 cd=3 2 1 1 0 0 cd=3 2 1 0 1 0 cd=3 2 1 0 0 0 cd=0 2 2 0 0 0 cd=4 1 -1 -1 -1 -1 cd=4 1 0 0 0 1 cd=4 1 0 1 0 0 cd=4 1 0 0 1 0 cd=4 1 0 0 0 0 cd=0 1 1 0 0 0 cd=4 0 0 0 0 0 cd=5
-F
Each facet of a polytope is displayed by listing its vertices in some basis for the sublattice carrying the facet. The result is not the affine normal form of the facet, however.
-G
If the input polytope P is a non-trivial multiple P = gQ of another polytope Q, the maximal proportionality factor g and P are displayed.
-L
This option results in the same calculations as the `-l' option (see above), but gives a more detailed output including the Witten index.
-U
If `-U' is specified without a number following (otherwise see below), it is computed whether the N lattice polytope has only simplicial facets; if this is not the case no further computations are performed on the polytope and no output results from it. (We are very grateful to Benjamin Nill for providing infomation for the `-U', `-C' and `-E' options.)
-U1
Like `-U' without number, but the facets now have to be unimodular (i.e. of volume 1). This corresponds to the case of Fano varieties.
-U5
This option is related to the classification of Fano polytopes (unimodular and simplicial reflexive polytopes) up to dimension five math/0702890. The corresponding data supplement contains examples of the usage of `-U5'.
-C1
This option was implemented for a search of Calabi-Yau threefolds which are related to previously known ones via conifold transitions arXiv:0802.3376. The use of PALP to produce these results is described at http://hep.itp.tuwien.ac.at/~kreuzer/CY/math/0802/. The input should be a 4-dimensional reflexive polytope P such that P * has only basic triangles or squares as two-dimensional faces. In this case the associated generic CY-hypersurface has isolated conifold singularities. The option " poly.x -C1" checks whether this 3-dimensional CY is smoothable.
-C2
The option -C2 was used to generate three-dimensional Fano hypersurfaces with conifold singularities, as described at arXiv:1203.6058. The input must be a reflexive 4-polytope that is divisible by 2, in which case the generic hypersurface associated to P / 2 is a three-dimensional Fano variety. A list of (hopefully all) such polytopes can be found at Max Kreuzer's site http://hep.itp.tuwien.ac.at/~kreuzer/CY/math/Fano/Fano.html, see the file "Reflexive2x.4d.gz". It is not clear how he obtained this list. Possibly he piped an extraction of the complete database of reflexive 4-polytopes through " poly.x -G" and then used some script to eliminate polytopes that are odd multiples of other polytopes. The program requires the input to be in matrix (rather than weight) format.
Example: " poly.x -C2" with input `8 1 1 1 1 4' crashes, but with the corresponding matrix input one gets
palp$ poly.x -C2 Degrees and weights `d1 w11 w12 ... d2 w21 w22 ...' or `#lines #columns' (= `PolyDim #Points' or `#Points PolyDim'): 4 5 Type the 20 coordinates as dim=4 lines with #pts=5 columns: -1 7 -1 -1 -1 -1 -1 7 -1 -1 -1 -1 -1 7 -1 -1 -1 -1 -1 1 pic=1 deg=64 h12= 0 rk=0 #sq=0 #dp=0 py=1 F=5 10 10 5 #Fano=1 4 5 Vertices of P* (N-lattice) M:201 5 N:7 5 1 0 0 0 -1 0 0 1 0 -1 0 1 0 0 -1 0 0 0 1 -4 P/2: 36 points (5 vertices) of P'=P/2 (M-lattice): P/2: 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 ... P/2: 0 0 4 0 0 1 2 3 0 1 2 3 0 1 2 0 1 0 1 2 ... P/2: 0 0 0 4 0 0 0 0 1 1 1 1 2 2 2 3 3 0 0 0 ... P/2: 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
-E
In the code " Polynf.c" there exists a procedure " Einstein\_Metric". It is called by the option " -e" of " nef.x". " poly.x -E" checks several symmetry properties of a reflexive polytope related to the set of roots of the associated toric variety. These are of interest with respect to the existence of Einstein-Kaehler metrics. Here, a root is a lattice point in the interior of a facet of the reflexive polytope (in the M lattice). Centrally-symmetric roots are called semisimple. If all roots are semisimple, then " ssroot=1". Only in this case PALP proceeds to check and display the following conditions: if the barycenter is 0 (" bary=1"), the sum of lattice points is 0 ("#Psum=1"), the sum of lattice points in each multiple is 0 ("#kPsum=1"), the group of lattice automorphisms has only the origin as a fixpoint ("#symm=1"). These conditions can be found explained in Chapter 5 (in particular, sections 5.5 and 5.6) of the dissertation of Benjamin Nill. This option cannot be combined with others; if `-E' is specified, all other options are ignored.